Đề thi giữa HK 2 Toán 11 Kết nối tri thức cấu trúc mới giải chi tiết-Đề 4 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
Phần 1. Câu trắc nghiệm nhiều phương án chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án đúng nhất.
Câu 1. Với $a$ là số thực dương tùy ý, biểu thức ${a^{\frac{5}{3}}} \cdot {a^{\frac{1}{3}}}$ là
A. ${a^5}$. B. ${a^{\bar 9}}$. C. ${a^{\frac{4}{3}}}$. D. ${a^2}$.
Câu 2. Với $a > 0,b > 0,\alpha ,\beta $ là các số thực bất kì, đẳng thức nào sau đây sai?
A. $\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha – \beta }}$. B. ${a^\alpha } \cdot {a^\beta } = {a^{\alpha + \beta }}$. C. $\frac{{{a^\alpha }}}{{{b^\beta }}} = {\left( {\frac{a}{b}} \right)^{\alpha – \beta }}$. D. ${a^\alpha } \cdot {b^\alpha } = {(ab)^\alpha }$.
Câu 3. Cho $a$ là số thực dương khác 1 . Mệnh đề nào dưới đây đúng với mọi số dương $x,y$ ?
A. ${log_a}\frac{x}{y} = {log_a}x – {log_a}y$ B. ${log_a}\frac{x}{y} = {log_a}\left( {x – y} \right)$ C. ${log_a}\frac{x}{y} = {log_a}x + {log_a}y$ D. ${log_a}\frac{x}{y} = \frac{{{log_a}x}}{{{log_a}y}}$
Câu 4. Cho $a > 0$ và $a \ne 1$, khi đó ${log_a}\sqrt[4]{a}$ bằng
A. 4 . B. $\frac{1}{4}$. C. $ – \frac{1}{4}$. D. -4 .
Câu 5. Tập xác định của hàm số $y = {log_2}x$ là
A. $\left[ {0; + \infty } \right)$. B. $\left( { – \infty ; + \infty } \right)$. C. $\left( {0; + \infty } \right)$. D. $\left[ {2; + \infty } \right)$.
Câu 6. Trong các hàm số sau hàm số nào nghịch biến trên $\mathbb{R}$ ?
A. ${log_3}{x^2}$ B. $y = log\left( {{x^3}} \right)$ C. $y = {\left( {\frac{e}{4}} \right)^x}$ D. $y = {\left( {\frac{2}{5}} \right)^{ – x}}$
Câu 7. Nghiệm của phương trình ${log_3}\left( {5x} \right) = 2$ là
A. $x = \frac{8}{5}$. B. $x = 9$. C. $x = \frac{9}{5}$. D. $x = 8$.
Câu 8. Tập nghiệm của bất phương trình ${2^x} < 5$ là
A. $\left( { – \infty ;{log_2}5} \right)$. B. $\left( {{log_2}5; + \infty } \right)$. C. $\left( { – \infty ;{log_5}2} \right)$. D. $\left( {{log_5}2; + \infty } \right)$.
Câu 9. Trong không gian, cho đường thẳng $d$ và điểm $O$. Qua $O$ có bao nhiêu đường thẳng vuông góc với đường thẳng $d$ ?
A. 3 . B. vô số. C. 1 . D. 2 .
Câu 10. Cho hình lập phương $ABCD \cdot A’B’C’D’$. Tính góc giữa hai đường thẳng $AC$ và $A’B$.
A. ${60^ \circ }$ B. ${45^ \circ }$ C. ${75^ \circ }$ D. ${90^ \circ }$
Câu 11. Cho hai đường thẳng phân biệt $a,b$ và mặt phẳng $\left( P \right)$, trong đó $a \bot \left( P \right)$. Chọn mệnh đề sai.
A. Nếu $b//a$ thì $b//\left( P \right)$. B. Nếu $b//a$ thì $b \bot \left( P \right)$.
C. Nếu $b \bot \left( P \right)$ thì $b//a$. D. Nếu $b//\left( P \right)$ thì $b \bot a$.
Câu 12. Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình vuông và $SA$ vuông góc đáy. Mệnh đề nào sau đây sai?
A. $BC \bot \left( {SAB} \right)$. B. $AC \bot \left( {SBD} \right)$. C. $BD \bot \left( {SAC} \right)$. D. $CD \bot \left( {SAD} \right)$.
Phần 2. Câu trắc nghiệm đúng sai. Thí sinh trả lời tù câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Câu 1. Cho các biểu thức sau: $P = {log_2}8 + {log_3}27 – {log_5}{5^3};Q = ln\left( {2e} \right) – log100$. Khi đó:
a) $P + Q = 2ln2$
b) $Q – P = ln2 – 4$
c) $3Q + P = 3ln2$
d) $2Q + P = 2ln2 + 1$
Câu 2. Giải được các phương trình sau. Khi đó:
a) Phương trình ${3^{x – 1}} = 9$ có một nghiệm
b) Phương trình ${5^{x – 1}} = {\left( {\frac{1}{{25}}} \right)^x}$ có nghiệm lớn hơn 3 .
c) Phương trình ${3^{x – 2}} = 6$ có chung tập nghiệm với phương trình ${x^2} – 2x + 4 = 0$
d) Phương trình ${7^{x + 2}} – {40.7^x} = 9$ có một nghiệm $x = a$, khi đó: $\mathop {\lim }\limits_{x \to a} ({x^2} + 2x + 5) = 6$
Câu 3. Cho hình lập phương $ABCD \cdot A’B’C’D’$. Khi đó:
a) $BD//B’D’$
b) $\left( {AC,B’D’} \right) = {90^ \circ }$
c) Tam giác $ACD’$ đều
d) $\left( {AC,A’B} \right) = {30^ \circ }$
Câu 4. Cho hình chóp $S \cdot ABCD$ có đáy là hình chữ nhật và $SA$ vuông góc với mặt phẳng đáy. Gọi $H,K$ theo thứ tự là hình chiếu của $A$ trên các cạnh $SB,SD$. Khi đó:
a) Tam giác $SBC$ vuông.
b) Tam giác $SCD$ vuông.
c) $SC \bot \left( {AHK} \right)$
d) $HK \bot SC$.
Phần 3. Câu trả lời ngắn. Thí sinh trả lời đáp án từ câu 1 đến câu 6.
Câu 1. Một người gửi 100 triệu đồng vào ngân hàng với lãi suất $8\% $ / năm. Biết rằng nếu người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Số tiền người đó nhận sau $n$ năm sẽ được tính theo công thức ${T_n} = 100{(1 + r)^n}$ (triệu đồng), trong đó $r\left( \% \right)$ là lãi suất và $n$ là số năm gửi tiền.
Hỏi số tiền lãi thu được của người đó sau 10 năm là bao nhiêu?
(Kết quả trong bài được tính chính xác đến hàng phần trăm)
Câu 2. Cho ${log_a}x = 3,{log_b}x = 4$ với $a > 1,b > 1,x > 1$. Tính $P = {log_{ab}}x$.
Câu 3. Tìm $m$ để hàm số $y = log\left( {{x^2} – 2mx + 4} \right)$ xác định với mọi $x$ thuộc $\mathbb{R}$.
Câu 4. Giả sử giá trị còn lại (tính theo triệu đồng) của một chiếc ô tô sau $t$ năm sử dụng được mô hình hoá bằng công thức: $V\left( t \right) = A \cdot {(0,905)^t}$, trong đó $A$ là giá xe (tính theo triệu đồng) lúc mới mua. Hỏi nếu theo mô hình này, sau bao nhiêu năm sử dụng thì giá trị của chiếc xe đó còn lại không quá 300 triệu đồng? (Làm tròn kết quả đến hàng đơn vị). Biết $A = 780$ (triệu đồng).
Câu 5. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a\sqrt 2 $, biết $SA = a,SC = a\sqrt 3 $. Gọi $M,N$ theo thứ tự là trung điểm các cạnh $AD,SD$. Tìm số đo của góc $\left( {MN,SC} \right)$.
Câu 6. Cho hình chóp $S.ABC$ có đáy là tam giác đều và mặt bên $\left( {SAB} \right)$ vuông góc với mặt phẳng đáy $\left( {ABC} \right)$. Gọi $H$ là trung điểm của $AB$. Tìm số đo của góc $\left( {CH,\left( {SAB} \right)} \right)$.
LỜI GIẢI CHI TIẾT
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời tù câu 1 đến câu 12. Mỗi câu hỏi thi sinh chỉ chọn một phuơng án đúng nhất.
Câu 1. Với $a$ là số thực dương tùy ý, biểu thức ${a^{\frac{5}{3}}} \cdot {a^{\frac{1}{3}}}$ là
A. ${a^5}$.
B. ${a^{\bar 9}}$.
C. ${a^{\frac{4}{3}}}$.
D. ${a^2}$.
Lời giải
Ta có ${a^{\frac{5}{3}}} \cdot {a^{\frac{1}{3}}} = {a^{\frac{5}{3} + \frac{1}{3}}} = {a^2}$
Câu 2. Với $a > 0,b > 0,\alpha ,\beta $ là các số thực bất kì, đẳng thức nào sau đây sai?
A. $\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha – \beta }}$.
B. ${a^\alpha } \cdot {a^\beta } = {a^{\alpha + \beta }}$.
C. $\frac{{{a^\alpha }}}{{{b^\beta }}} = {\left( {\frac{a}{b}} \right)^{\alpha – \beta }}$.
D. ${a^\alpha } \cdot {b^\alpha } = {(ab)^\alpha }$.
Lời giải
Chọn C
Câu 3. Cho $a$ là số thực dương khác 1 . Mệnh đề nào dưới đây đúng với mọi số dương $x,y$ ?
A. ${log_a}\frac{x}{y} = {log_a}x – {log_a}y$
B. ${log_a}\frac{x}{y} = {log_a}\left( {x – y} \right)$
C. ${log_a}\frac{x}{y} = {log_a}x + {log_a}y$
D. ${log_a}\frac{x}{y} = \frac{{{log_a}x}}{{{log_a}y}}$
Lời giải
Chọn A
Theo tính chất của logarit.
Câu 4. Cho $a > 0$ và $a \ne 1$, khi đó ${log_a}\sqrt[4]{a}$ bằng
A. 4 .
B. $\frac{1}{4}$.
C. $ – \frac{1}{4}$.
D. -4 .
Lời giải
Chọn B
Ta có: ${log_a}\sqrt[4]{a} = {log_a}{a^{\frac{1}{4}}} = \frac{1}{4}$.
Câu 5. Tập xác định của hàm số $y = {log_2}x$ là
A. $\left[ {0; + \infty } \right)$.
B. $\left( { – \infty ; + \infty } \right)$.
C. $\left( {0; + \infty } \right)$.
D. $\left[ {2; + \infty } \right)$.
Lời giải
Chọn C
Điều kiện xác định của hàm số $y = {log_2}x$ là $x > 0$.
Vậy tập xác định của hàm số $y = {log_2}x$ là $D = \left( {0; + \infty } \right)$.
Câu 6. Trong các hàm số sau hàm số nào nghịch biến trên $\mathbb{R}$ ?
A. ${log_3}{x^2}$
B. $y = log\left( {{x^3}} \right)$
C. $y = {\left( {\frac{e}{4}} \right)^x}$
D. $y = {\left( {\frac{2}{5}} \right)^{ – x}}$
Lời giải
Chọn C
Hàm số mũ $y = {a^x}$ với $0 < a < 1$ nghịch biến trên $\mathbb{R}$.
Ta có $0 < \frac{e}{4} < 1$ nên hàm số $y = {\left( {\frac{e}{4}} \right)^x}$ nghịch biến trên $\mathbb{R}$.
Câu 7. Nghiệm của phương trình ${log_3}\left( {5x} \right) = 2$ là
A. $x = \frac{8}{5}$.
B. $x = 9$.
C. $x = \frac{9}{5}$.
D. $x = 8$.
Lời giải
Chọn C
ТХĐ: $D = \left( {0; + \infty } \right)$.
Ta có: ${log_3}\left( {5x} \right) = 2 \Leftrightarrow 5x = {3^2} \Leftrightarrow x = \frac{9}{5}$.
Câu 8. Tập nghiệm của bất phương trình ${2^x} < 5$ là
A. $\left( { – \infty ;{log_2}5} \right)$.
B. $\left( {{log_2}5; + \infty } \right)$.
C. $\left( { – \infty ;{log_5}2} \right)$.
D. $\left( {{log_5}2; + \infty } \right)$.
Lời giải
Chọn A
Ta có: ${2^x} < 5 \Leftrightarrow x < {log_2}5$
Vậy tập nghiệm $S = \left( { – \infty ;{log_2}5} \right)$.
Câu 9. Trong không gian, cho đường thẳng $d$ và điểm $O$. Qua $O$ có bao nhiêu đường thẳng vuông góc với đường thẳng $d$ ?
A. 3 .
B. vô số.
C. 1 .
D. 2 .
Chọn B
Lời giải
Trong không gian, có vô số đường thẳng qua một điểm cho trước và vuông góc với một đường thẳng cho trước. Vì vậy chọn đáp án B
Câu 10. Cho hình lập phương $ABCD \cdot A’B’C’D’$. Tính góc giữa hai đường thẳng $AC$ và $A’B$.
A. ${60^ \circ }$
B. ${45^ \circ }$
C. ${75^ \circ }$
D. ${90^ \circ }$
Chọn A
Lời giải
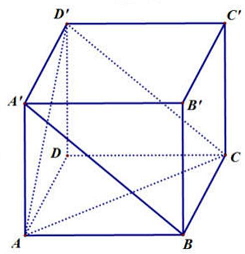
Do $A’BCD’$ là hình bình hành nên $A’B//D’C$.
Suy ra góc giữa hai đường thẳng $AC$ và $A’B$ bằng góc giữa hai đường thẳng $AC$ và $D’C$ và đó chính là góc $\widehat {ACD’} = {60^ \circ }$ (do $\vartriangle ACD’$ đều).
Câu 11. Cho hai đường thẳng phân biệt $a,b$ và mặt phẳng $\left( P \right)$, trong đó $a \bot \left( P \right)$. Chọn mệnh đề sai.
A. Nếu $b//a$ thì $b//\left( P \right)$.
B. Nếu $b//a$ thì $b \bot \left( P \right)$.
C. Nếu $b \bot \left( P \right)$ thì $b//a$.
D. Nếu $b//\left( P \right)$ thì $b \bot a$.
Lời giải
Nếu $a \bot \left( P \right)$ và $b//a$ thì $b \bot \left( P \right)$.
Câu 12. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông và $SA$ vuông góc đáy. Mệnh đề nào sau đây sai?
A. $BC \bot \left( {SAB} \right)$.
B. $AC \bot \left( {SBD} \right)$.
C. $BD \bot \left( {SAC} \right)$.
D. $CD \bot \left( {SAD} \right)$.
Lời giải
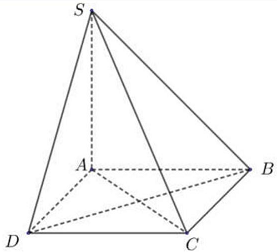
Ta có:
$ + \left\{ {\begin{array}{*{20}{l}}
{BC \bot AB} \\
{BC \bot SA}
\end{array} \Rightarrow BC \bot \left( {SAB} \right)} \right.$.
$ + \left\{ {\begin{array}{*{20}{l}}
{CD \bot AD} \\
{CD \bot SA}
\end{array} \Rightarrow CD \bot \left( {SAD} \right)} \right.$.
$ + \left\{ {\begin{array}{*{20}{l}}
{BD \bot AC} \\
{BD \bot SA}
\end{array} \Rightarrow BD \bot \left( {SAC} \right)} \right.$.
Suy ra: đáp án B sai.
Phần 2. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗ ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Câu 1. Cho các biểu thức sau: $P = {log_2}8 + {log_3}27 – {log_5}{5^3};Q = ln\left( {2e} \right) – log100$. Khi đó:
a) $P + Q = 2ln2$
b) $Q – P = ln2 – 4$
c) $3Q + P = 3ln2$
d) $2Q + P = 2ln2 + 1$
Lời giải
a) Sai
b) Đúng
c) Đúng
d) Đúng
Ta có: $P = {log_2}8 + {log_3}27 – {log_5}{5^3} = {log_2}{2^3} + {log_3}{3^3} – {log_5}{5^3} = 3 + 3 – 3 = 3$.
Ta có: $Q = ln\left( {2e} \right) – log100 = ln2 + lne – log{10^2} = ln2 + 1 – 2 = ln2 – 1$.
Câu 2. Giải được các phương trình sau. Khi đó:
a) Phương trình ${3^{x – 1}} = 9$ có một nghiệm
b) Phương trình ${5^{x – 1}} = {\left( {\frac{1}{{25}}} \right)^x}$ có nghiệm lớn hơn 3 .
c) Phương trình ${3^{x – 2}} = 6$ có chung tập nghiệm với phương trình ${x^2} – 2x + 4 = 0$
d) Phương trình ${7^{x + 2}} – {40.7^x} = 9$ có một nghiệm $x = a$, khi đó: $\mathop {\lim }\limits_{x \to a} ({x^2} + 2x + 5) = 6$
Lời giải
a) Đúng
b) Sai
c) Sai
d) Sai
a) ${3^{x – 1}} = 9 \Leftrightarrow {3^{x – 1}} = {3^2} \Leftrightarrow x – 1 = 2 \Leftrightarrow x = 3$.
Vậy phương trình có nghiệm là $x = 3$.
b) ${5^{x – 1}} = {\left( {\frac{1}{{25}}} \right)^x} \Leftrightarrow {5^{x – 1}} = {5^{ – 2x}} \Leftrightarrow x – 1 = – 2x \Leftrightarrow x = \frac{1}{3}$.
Vậy phương trình có nghiệm là $x = \frac{1}{3}$.
c) ${3^{x – 2}} = 6 \Leftrightarrow x – 2 = {log_3}6 \Leftrightarrow x = {log_3}6 + 2$.
Vậy phương trình có nghiệm là $x = {log_3}6 + 2$.
d) ${7^{x + 2}} – {40.7^x} = 9 \Leftrightarrow {7^2}{.7^x} – {40.7^x} = 9 \Leftrightarrow {9.7^x} = 9 \Leftrightarrow {7^x} = 1 \Leftrightarrow x = 0$.
Vậy phương trình có nghiệm là $x = 0$.
Suy ra, $\mathop {\lim }\limits_{x \to a} ({x^2} + 2x + 5) = \mathop {\lim }\limits_{x \to 0} ({x^2} + 2x + 5) = 5$
Câu 3. Cho hình lập phương $ABCD \cdot A’B’C’D’$. Khi đó:
a) $BD//B’D’$
b) $\left( {AC,B’D’} \right) = {90^ \circ }$
c) Tam giác $ACD’$ đều
d) $\left( {AC,A’B} \right) = {30^ \circ }$
Lời giải
a) Đúng
b) Đúng
c) Đúng
d) Sai
Ta có: $BB’//DD’,BB’ = DD’ \Rightarrow BDD’B’$ là hình bình hành $ \Rightarrow BD//B’D’$.
Vì vậy $\left( {AC,B’D’} \right) = \left( {AC,BD} \right) = {90^ \circ }$ (do $AC$ và $BD$ là hai đường chéo hình vuông $ABCD$ ).
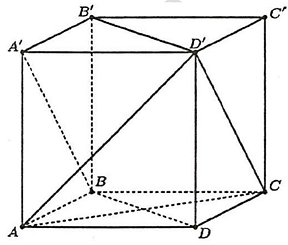
Ta có: $A’D’//BC,A’D’ = BC \Rightarrow A’BCD’$ là hình bình hành $ \Rightarrow A’B//CD’$.
Vì vậy $\left( {AC,A’B} \right) = \left( {AC,CD’} \right)$.
Gọi $a$ là cạnh của hình lập phương thì $AD’ = CD’ = AC = a\sqrt 2 $ (đường chéo của hình vuông cạnh $a$ ).
Suy ra tam giác $ACD’$ dều nên $\left( {AC,CD’} \right) = \widehat {ACD’} = {60^ \circ }$.
Vậy $\left( {AC,A’B} \right) = {60^ \circ }$.
Câu 4. Cho hình chóp $S \cdot ABCD$ có đáy là hình chữ nhật và $SA$ vuông góc với mặt phẳng đáy. Gọi $H,K$ theo thứ tự là hình chiếu của $A$ trên các cạnh $SB,SD$. Khi đó:
a) Tam giác $SBC$ vuông.
b) Tam giác $SCD$ vuông.
c) $SC \bot \left( {AHK} \right)$
d) $HK \bot SC$.
Lời giải
a) Đúng
b) Đúng
c) Đúng
d) Đúng
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{BC \bot AB} \\
{BC \bot SA\left( {\;do\;SA \bot \left( {ABCD} \right)} \right)}
\end{array} \Rightarrow BC \bot \left( {SAB} \right)} \right.$.
Vì $\left\{ {\begin{array}{*{20}{l}}
{BC \bot \left( {SAB} \right)} \\
{SB \subset \left( {SAB} \right)}
\end{array} \Rightarrow BC \bot SB} \right.$ hay $\vartriangle SBC$ vuông tại $B$.
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{CD \bot AD} \\
{CD \bot SA\left( {\;do\;SA \bot \left( {ABCD} \right)} \right)}
\end{array} \Rightarrow CD \bot \left( {SAD} \right)} \right.$.
Vì $\left\{ {\begin{array}{*{20}{l}}
{CD \bot \left( {SAD} \right)} \\
{SD \subset \left( {SAD} \right)}
\end{array} \Rightarrow CD \bot SD} \right.$ hay $\vartriangle SCD$ vuông tại $D$.
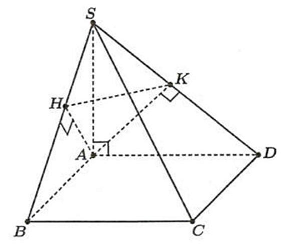
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{AH \bot SB} \\
{AH \bot BC\left( {\;do\;BC \bot \left( {SAB} \right)} \right)}
\end{array}} \right.$ $ \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC$. (1)
Tương tự: $\left\{ {\begin{array}{*{20}{l}}
{AK \bot SD} \\
{AK \bot CD\left( {\;do\;CD \bot \left( {SAD} \right)} \right)}
\end{array}} \right.$$ \Rightarrow AK \bot \left( {SCD} \right) \Rightarrow AK \bot SC$. (2)
Từ (1) và (2) suy ra $SC \bot \left( {AHK} \right)$, mà $HK \subset \left( {AHK} \right)$ nên $HK \bot SC$.
Phần 3. Câu trả lời ngắn. Thí sinh trả lời đáp án từ câu 1 đến câu 6.
Câu 1. Một người gửi 100 triệu đồng vào ngân hàng với lãi suất $8\% $ / năm. Biết rằng nếu người đó không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo. Số tiền người đó nhận sau $n$ năm sẽ được tính theo công thức ${T_n} = 100{(1 + r)^n}$ (triệu đồng), trong đó $r\left( \% \right)$ là lãi suất và $n$ là số năm gửi tiền.
Hỏi số tiền lãi thu được của người đó sau 10 năm là bao nhiêu?
(Kết quả trong bài được tính chính xác đến hàng phần trăm)
Lời giải
Số tiền người đó nhận sau 10 năm là: ${T_{10}} = 100{\left( {1 + \frac{8}{{100}}} \right)^{10}} \approx 215,89$ (triệu đồng).
Số tiền lãi sau 10 năm gửi tiền xấp xỉ là: $215,89 – 100 = 115,89$ (triệu đồng).
Câu 2. Cho ${log_a}x = 3,{log_b}x = 4$ với $a > 1,b > 1,x > 1$. Tính $P = {log_{ab}}x$.
Lời giải
Ta có: $P = {log_{ab}}x = \frac{1}{{{log_x}\left( {ab} \right)}}$
$ = \frac{1}{{{log_x}a + {log_x}b}} = \frac{1}{{\frac{1}{3} + \frac{1}{4}}} = \frac{{12}}{7}$.
Câu 3. Tìm $m$ để hàm số $y = log\left( {{x^2} – 2mx + 4} \right)$ xác định với mọi $x$ thuộc $\mathbb{R}$.
Lời giải
Hàm số xác định với mọi $x \in \mathbb{R} \Leftrightarrow {x^2} – 2mx + 4 > 0,\forall x \in \mathbb{R}$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = 1 > 0} \\
{\Delta ‘ = {m^2} – 4 < 0}
\end{array} \Leftrightarrow – 2 < m < 2} \right.$.
Vậy $ – 2 < m < 2$ thoả mãn đề bài.
Câu 4. Giả sử giá trị còn lại (tính theo triệu đồng) của một chiếc ô tô sau $t$ năm sử dụng được mô hình hoá bằng công thức: $V\left( t \right) = A \cdot {(0,905)^t}$, trong đó $A$ là giá xe (tính theo triệu đồng) lúc mới mua. Hỏi nếu theo mô hình này, sau bao nhiêu năm sử dụng thì giá trị của chiếc xe đó còn lại không quá 300 triệu đồng? (Làm tròn kết quả đến hàng đơn vị). Biết $A = 780$ (triệu đồng).
Lời giải
Ta có: $V\left( t \right) \leqslant 300 \Leftrightarrow 780.{(0,905)^t} \leqslant 300$
$ \Leftrightarrow {(0,905)^t} \leqslant \frac{5}{{13}} \Leftrightarrow t \geqslant {log_{0,905}}\left( {\frac{5}{{13}}} \right) \approx 9,6$ (do $0 < 0,905 < 1)$.
Vậy sau khoảng 10 năm sử dụng, giá trị chiếc xe đó còn lại không quá 300 triệu đồng.
Câu 5. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a\sqrt 2 $, biết $SA = a,SC = a\sqrt 3 $. Gọi $M,N$ theo thứ tự là trung điểm các cạnh $AD,SD$. Tìm số đo của góc $\left( {MN,SC} \right)$.
Lời giải
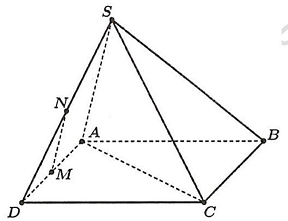
Vì $MN$ là đường trung bình của tam giác $SAD$ nên $MN//SA \Rightarrow \left( {MN,SC} \right) = \left( {SA,SC} \right)$.
Tam giác $ABC$ vuông tại $B$ có:
$\begin{array}{*{20}{r}}
{AC}&{\; = \sqrt {A{B^2} + B{C^2}} } \\
{}&{\; = \sqrt {{{(a\sqrt 2 )}^2} + {{(a\sqrt 2 )}^2}} = 2a.}
\end{array}$
Xét tam giác $SAC$, ta có:
$S{A^2} + S{C^2} = A{C^2}\left( {} \right.$ do $\left. {{a^2} + {{(a\sqrt 3 )}^2} = {{(2a)}^2}} \right)$
Suy ra tam giác $SAC$ vuông tại $S$.
Vậy $\left( {MN,SC} \right) = \left( {SA,SC} \right) = {90^ \circ }$ hay $MN \bot SC$.
Câu 6. Cho hình chóp $S.ABC$ có đáy là tam giác đều và mặt bên $\left( {SAB} \right)$ vuông góc với mặt phẳng đáy $\left( {ABC} \right)$. Gọi $H$ là trung điểm của $AB$. Tìm số đo của góc $\left( {CH,\left( {SAB} \right)} \right)$.
Lời giải
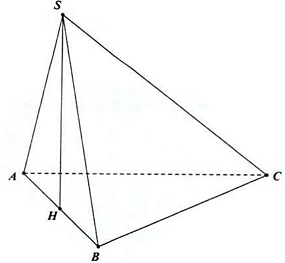
Vì $\vartriangle ABC$ dều mà $H$ là trung điểm $AB$ nên $CH \bot AB$. Mà $\left( {SAB} \right) \cap \left( {ABC} \right) = AB$ và $\left( {SAB} \right) \bot \left( {ABC} \right)$ nên $CH \bot \left( {SAB} \right)$.














_HasThumb.png)

