Đề Thi Giữa Học Kì 2 Toán 10 Kết Nối Tri Thức Cấu Trúc Mới Giải Chi Tiết-Đề 1

Đề thi giữa học kì 2 Toán 10 Kết nối tri thức cấu trúc mới giải chi tiết-Đề 1 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mối câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Điểm nào sau đây thuộc đồ thị hàm số $y = 2x + 1$.

A. $A\left( {1;2} \right)$.

B. $B\left( {1;1} \right)$.

C. $B\left( {2; – 4} \right)$.

D. $D\left( { – 1; – 1} \right)$.

Câu 2: Tìm tập xác định của hàm số $y = \frac{{x + 2026}}{{{x^2} – 2025x + 2024}}$

A. $D = \mathbb{R}$.

B. $D = \left( {1;2024} \right)$.

C. $D = \left( {2024; + \infty } \right)$.

D. $D = \mathbb{R} \setminus \left\{ {1;2024} \right\}$.

Câu 3: Cho tam thức $f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)$ có $\Delta = {b^2} – 4ac$. Ta có $f\left( x \right) \leqslant 0$ với $\forall x \in \mathbb{R}$ khi và chỉ khi:

A. $\left\{ {\begin{array}{*{20}{l}}
{a < 0} \\
{\Delta \leqslant 0}
\end{array}} \right.$.

B. $\left\{ {\begin{array}{*{20}{l}}
{a \leqslant 0} \\
{\Delta < 0}
\end{array}} \right.$.

C. $\left\{ {\begin{array}{*{20}{l}}
{a < 0} \\
{\Delta \geqslant 0}
\end{array}} \right.$.

D. $\left\{ {\begin{array}{*{20}{l}}
{a > 0} \\
{\Delta \leqslant 0}
\end{array}} \right.$.

Câu 4: Cho tam thức $f\left( x \right) = {x^2} – 8x + 16$. Khẳng định nào sau đây là đúng?

A. $f\left( x \right) < 0$ khi $x \ne 4$.

B. $f\left( x \right) > 0$ với mọi $x \in \mathbb{R}$.

C. $f\left( x \right) \geqslant 0$ với mọi $x \in \mathbb{R}$.

D. $f\left( x \right) < 0$ khi $x < 4$.

Câu 5: Tập nghiệm của bất phương trình $2{x^2} – 14x + 20 < 0$ là

A. $S = \left( { – \infty ;2\left] \cup \right[5; + \infty } \right)$.

B. $S = \left( { – \infty ;2} \right) \cup \left( {5; + \infty } \right)$.

C. $S = \left( {2;5} \right)$.

D. $S = \left[ {2;5} \right]$.

Câu 6: Nghiệm của phương trình $\sqrt {{x^2} – 4x – 12} = x – 4$ là

A. $x = – 7$.

B. $x = 7$.

C. $x = 1$.

D. $x = – 1$.

Câu 7: Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng $d:x – 2y + 3 = 0$. Vectơ pháp tuyến của đường thẳng $d$ là

A. $\vec n = \left( {1; – 2} \right)$.

B. $\vec n = \left( {2;1} \right)$.

C. $\vec n = \left( { – 2;3} \right)$.

D. $\vec n = \left( {1;3} \right)$.

Câu 8: Viết phương trình đường thẳng $\left( d \right)$ đi qua $M\left( { – 2;3} \right)$ và có VTCP $\vec u = \left( {1; – 4} \right)$.

A. $\left\{ {\begin{array}{*{20}{l}}
{x = – 2 + 3t} \\
{y = 1 – 4t}
\end{array}} \right.$.

B. $\left\{ {\begin{array}{*{20}{l}}
{x = – 2 + t} \\
{y = 3 – 4t}
\end{array}} \right.$.

C. $\left\{ {\begin{array}{*{20}{l}}
{x = 1 – 2t} \\
{y = – 4 + 3t}
\end{array}} \right.$.

D. $\left\{ {\begin{array}{*{20}{l}}
{x = 3 – 2t} \\
{y = – 4 + t}
\end{array}} \right.$

Câu 9: Trong mặt phẳng $Oxy$, khoảng cách từ gốc tọa độ $O$ đến đường thẳng $d:4x – 3y + 1 = 0$ bằng

A. 3 .

B. 4 .

C. 1 .

D. $\frac{1}{5}$.

Câu 10: Trong mặt phẳng tọa độ $Oxy$, tính góc giữa 2 đường thẳng ${d_1}:x – \sqrt 3 y + \sqrt 7 = 0$ và ${d_2}$ : $\left\{ {\begin{array}{*{20}{l}}
{x = t} \\
{y = 4}
\end{array}} \right.$

A. ${90^ \circ }$.

B. ${60^ \circ }$.

C. ${45^0}$.

D. ${30^ \circ }$.

Câu 11: Trong mặt phẳng tọa độ $Oxy$, phương trình nào dưới đây là phương trình đường tròn?

A. ${x^2} + 2{y^2} – 2x + 4y – 1 = 0$.

B. ${x^2} – {y^2} + 4x – 6y – 2 = 0$.

C. ${x^2} + {y^2} + x + y + 4 = 0$.

D. ${x^2} + {y^2} – 4x – 1 = 0$.

Câu 12: Trong mặt phẳng tọa độ $Oxy$, cho đường tròn $\left( C \right)$ có phương trình ${x^2} + {y^2} – 2x + 4y – 4 = 0$. Tâm $I$ và bán kính $R$ của $\left( C \right)$ lần lượt là

A. $I\left( {1; – 2} \right),R = 1$.

B. $I\left( {1; – 2} \right),R = 3$.

C. $I\left( {1; – 2} \right),R = 9$.

D. $I\left( {2; – 4} \right),R = 3$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho bảng biến thiên của hàm số bậc hai $y = a{x^2} + bx + c$. Xét tính đúng sai của các mệnh đề sau:

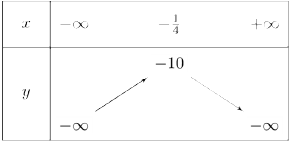
a) Hàm số đã cho nghịch biến trên khoảng $\left( {2; + \infty } \right)$.

b) Hệ số $a$ của hàm số bậc hai đã cho là một số dương

c) Hàm số đã cho đồng biến trên khoảng $\left( { – \frac{1}{4};2} \right)$.

d) Giá trị lớn nhất của hàm số bằng -10

Câu 2: Trong mặt phẳng với hệ tọa độ $Oxy$, cho tam giác $ABC$ có phương trình cạnh $AB$ là $x – y – 2 = 0$, phương trình cạnh $AC$ là $x + 2y – 5 = 0$. Biết trọng tâm của tam giác là điểm $G\left( {3;2} \right)$.

a) Phương trình cạnh $AB$ và phương trình cạnh $AC$ có cùng một vectơ pháp tuyến.

b) Tọa độ của điểm $A$ là $A\left( {3;1} \right)$

c) Hoành độ của điểm $C$ là một số nguyên âm

d) Phương trình đường thẳng cạnh $BC$ là $x – 4y + 7 = 0$

Câu 3: Công ty $A$ có 100 cán bộ công nhân viên và muốn tổ chức cho toàn công ty đi Year End Party tại khu du lịch Tam Đảo, Vĩnh Phúc. Một công ty du lịch chào giá vé với công ty A như sau:

Với 40 khách hàng đầu tiên có giá vé là 3 triệu đồng/người.

Nếu có nhiều hơn 40 người đăng kí thì cứ thêm 1 người giá vé sẽ giảm 15000 đồng/người cho toàn bộ hành khách.

Gọi $x$ là số lượng cán bộ công nhân viên của công ty $A$ đăng kí thứ 41 trở lên. Biết chi phí thực tế công ty dành cho mỗi khách hàng là 1,95 triệu đồng.

a) Giá vé còn lại sau khi thêm $x$ người là: 3000 – $15x$ (nghìn đồng/ người)

b) Chi phí thực tế cho chuyến đi này là: 1950(40 – x) (nghìn đồng)

c) Lợi nhuận của công ty du lịch đạt được biểu thị bằng công thức $T = 15{x^2} – 450x + 42000$ (nghìn đồng)

d) Số cán bộ công nhân viên công ty $A$ đăng ký tối thiểu là 50 người thì công ty du lịch đạt lợi nhuận tối thiểu 45 triệu đồng.

Câu 4: Trong mặt phẳng $Oxy$, cho điểm $A\left( {1; – 3} \right)$ và đường thẳng $d:2x – 3y + 5 = 0$. Gọi $\Delta $ là đường thẳng đi qua điểm $A$ và tạo với đường thẳng $d$ một góc ${45^ \circ }$.

a) Một vectơ pháp tuyến của đường thẳng $d$ là $\overrightarrow {{n_d}} = \left( {2;3} \right)$

b) Khoảng cách từ điểm $A$ đến đường thẳng $d$ bằng $\frac{{\sqrt {13} }}{{13}}$

c) Đường thẳng $\Delta $ có một vectơ pháp tuyến là $\overrightarrow {{n_\Delta }} = \left( {1;5} \right)$

d) Có hai đường thẳng $\Delta $ thỏa mãn yêu cầu bài toán đặt ra.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Tìm số giao điểm giữa đồ thị hàm số $y = \sqrt {2x – 3} $ và đường thẳng $y = 3 – x$

Đáp án:

Câu 2: Cho tam thức bậc hai $f\left( x \right) = {x^2} – \left( {2m + 3} \right)x + {m^2} + 3m$, $m$ là tham số. Có bao nhiêu giá trị nguyên của tham số $m$ để $f\left( x \right) < 0,\forall x \in \left( { – 1;0} \right)$.

Đáp án:

Câu 3: Độ giảm huyết áp của một bệnh nhân được cho bởi công thức $G\left( x \right) = 0,3x\left( {12 – x} \right)$, trong đó $x$ là liều lượng thuốc được tiêm cho bệnh nhân ( $x$ được tính bằng miligam). Tính liều lượng thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.

Câu 4: Cho tam giác $ABC$ với $A\left( { – 1; – 2} \right)$ và phương trình đường thẳng chứa cạnh $BC$ là $x – y + 4 = 0$ Phương trình đường trung bình ứng với cạnh đáy $BC$ của tam giác có dạng $ax + by + c = 0$. Hãy tính giá trị của biểu thức $T = a + b + c$.

Đáp án:

Câu 5: Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng $\Delta :ax + by + 4 = 0\left( {a,b \in \mathbb{N}} \right)$ đi qua điểm $M\left( { – 1; – 2} \right)$ và tạo với đường thẳng $d:x + 3y – 3 = 0$ một góc $\frac{\pi }{4}$. Giá trị biểu thức $P = a + b$ bằng

Đáp án:

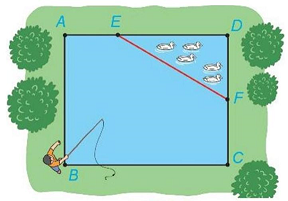
Câu 6: Một ao cá có dạng hình chữ nhật $ABCD$ với chiều dài $AD = 17\;m$, chiều rộng $AB = 13\;m$. Phần tam giác $DEF$ người ta để nuôi vịt, biết $AE = 6\;m,CF = 6,5\;m$ (minh họa như hình vẽ). Tính khoảng cách từ vị trí người đứng ở vị trí $B$ câu cá đến vách ngăn nuôi vịt là đường thẳng EF (Kết quả làm tròn đến hàng phần trăm).

Đáp án:

ĐÁP ÁN VÀ GIẢI CHI TIẾT

PHẦN I.

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Chọn	D	D	A	C	C	B	A	B	D	D	D	B

PHẦN II.

Câu 1	Câu 2	Câu 3	Câu 4
a) Đ	a) S	a) Đ	a) S
b) S	b) Đ	b) S	b) S

c) S	c) S	c) S	c) Đ
d) Đ	d) Đ	d) Đ	d) Đ

PHẦN III.

Câu	1	2	3	4	5	6
Chọn	1	3	6	3	3	14,24

LỜI GIẢI CHI TIẾT

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Điểm nào sau đây thuộc đồ thị hàm số $y = 2x + 1$.

A. $A\left( {1;2} \right)$.

B. $B\left( {1;1} \right)$.

C. $B\left( {2; – 4} \right)$.

D. $D\left( { – 1; – 1} \right)$.

Lời giải

Thay $x = – 1;y = – 1$ vào hàm số $y = 2x + 1$ ta có $ – 1 = 2.\left( { – 1} \right) + 1 \Leftrightarrow – 1 = – 1$.

Vậy điểm $D\left( { – 1; – 1} \right)$ thuộc đồ thị hàm số $y = 2x + 1$.

Câu 2: Tìm tập xác định của hàm số $y = \frac{{x + 2026}}{{{x^2} – 2025x + 2024}}$

A. $D = \mathbb{R}$.

B. $D = \left( {1;2024} \right)$.

C. $D = \left( {2024; + \infty } \right)$.

D. $D = \mathbb{R} \setminus \left\{ {1;2024} \right\}$.

Lời giải

Điều kiện xác định của hàm số là ${x^2} – 2025x + 2024 \ne 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x \ne 1} \\
{x \ne 2024}
\end{array}} \right.$.

Vậy tập xác định của hàm số $y = \frac{{x + 2026}}{{{x^2} – 2025x + 2024}}$ là $D = \mathbb{R} \setminus \left\{ {1;2024} \right\}$.

Câu 3: Cho tam thức $f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)$ có $\Delta = {b^2} – 4ac$. Ta có $f\left( x \right) \leqslant 0$ với $\forall x \in \mathbb{R}$ khi và chỉ khi:

A. $\left\{ {\begin{array}{*{20}{l}}
{a < 0} \\
{\Delta \leqslant 0}
\end{array}} \right.$.

B. $\left\{ {\begin{array}{*{20}{l}}
{a \leqslant 0} \\
{\Delta < 0}
\end{array}} \right.$.

C. $\left\{ {\begin{array}{*{20}{l}}
{a < 0} \\
{\Delta \geqslant 0}
\end{array}} \right.$.

D. $\left\{ {\begin{array}{*{20}{l}}
{a > 0} \\
{\Delta \leqslant 0}
\end{array}} \right.$.

Lời giải

Áp dụng định lý về dấu của tam thức bậc hai ta có: $f\left( x \right) \leqslant 0$ với $\forall x \in \mathbb{R}$ khi và chỉ khi $\left\{ {\begin{array}{*{20}{l}}
{a < 0} \\
{\Delta \leqslant 0}
\end{array}} \right.$

Câu 4: Cho tam thức $f\left( x \right) = {x^2} – 8x + 16$. Khẳng định nào sau đây là đúng?

A. $f\left( x \right) < 0$ khi $x \ne 4$.

B. $f\left( x \right) > 0$ với mọi $x \in \mathbb{R}$.

C. $f\left( x \right) \geqslant 0$ với mọi $x \in \mathbb{R}$.

D. $f\left( x \right) < 0$ khi $x < 4$.

Biểu thức đã cho là tam thức bậc hai có $\Delta = {( – 8)^2} – 4.16 = 0$, hệ số $a = 1 > 0$ nên $f\left( x \right) \geqslant 0$ với mọi $x \in \mathbb{R}$.

Câu 5: Tập nghiệm của bất phương trình $2{x^2} – 14x + 20 < 0$ là

A. $S = \left( { – \infty ;2\left] \cup \right[5; + \infty } \right)$.

B. $S = \left( { – \infty ;2} \right) \cup \left( {5; + \infty } \right)$.

C. $S = \left( {2;5} \right)$.

D. $S = \left[ {2;5} \right]$.

Lời giải

Đặt $f\left( x \right) = 2{x^2} – 14x + 20$, bảng xét dấu

Suy ra tập nghiệm của bất phương trình là $S = \left( {2;5} \right)$.

Câu 6: Nghiệm của phương trình $\sqrt {{x^2} – 4x – 12} = x – 4$ là

A. $x = – 7$.

B. $x = 7$.

C. $x = 1$.

D. $x = – 1$.

Lời giải

Thay lần lượt 4 giá trị của $x$ ở 4 đáp án vào phương trình đã cho ta thấy chỉ có $x = 5$ thoả mãn phương trình. Vậy $x = 7$ là nghiệm của phương trình.

Câu 7: Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng $d:x – 2y + 3 = 0$. Vectơ pháp tuyến của đường thẳng $d$ là

A. $\vec n = \left( {1; – 2} \right)$.

B. $\vec n = \left( {2;1} \right)$.

C. $\vec n = \left( { – 2;3} \right)$.

D. $\vec n = \left( {1;3} \right)$.

Lời giải

Đường thẳng $d:x – 2y + 3 = 0$ có VTPT là $\vec n = \left( {1; – 2} \right)$.

Câu 8: Viết phương trình đường thẳng $\left( d \right)$ đi qua $M\left( { – 2;3} \right)$ và có VTCP $\vec u = \left( {1; – 4} \right)$.

A. $\left\{ {\begin{array}{*{20}{l}}
{x = – 2 + 3t} \\
{y = 1 – 4t}
\end{array}} \right.$.

B. $\left\{ {\begin{array}{*{20}{l}}
{x = – 2 + t} \\
{y = 3 – 4t}
\end{array}} \right.$.

C. $\left\{ {\begin{array}{*{20}{l}}
{x = 1 – 2t} \\
{y = – 4 + 3t}
\end{array}} \right.$.

D. $\left\{ {\begin{array}{*{20}{l}}
{x = 3 – 2t} \\
{y = – 4 + t}
\end{array}} \right.$

Lời giải

Phương trình tham số của đường thẳng $D$ là $\left\{ {\begin{array}{*{20}{l}}
{x = – 2 + t} \\
{y = 3 – 4t}
\end{array}} \right.$

Câu 9: Trong mặt phẳng $Oxy$, khoảng cách từ gốc tọa độ $O$ đến đường thẳng $d:4x – 3y + 1 = 0$ bằng

A. 3 .

B. 4 .

C. 1 .

D. $\frac{1}{5}$.

Lời giải

Ta có $d\left( {O,d} \right) = \frac{{\left| {4 \cdot 0 – 3 \cdot 0 + 1} \right|}}{{\sqrt {{4^2} + {3^2}} }} = \frac{1}{5}$.

Câu 10: Trong mặt phẳng tọa độ $Oxy$, tính góc giữa 2 đường thẳng ${d_1}:x – \sqrt 3 y + \sqrt 7 = 0$ và ${d_2}$ : $\left\{ {\begin{array}{*{20}{l}}
{x = t} \\
{y = 4}
\end{array}} \right.$

A. ${90^ \circ }$.

B. ${60^ \circ }$.

C. ${45^0}$

D. ${30^ \circ }$.

Lời giải

${d_1}$ có một vectơ pháp tuyến là $\overrightarrow {{n_1}} = \left( {1; – \sqrt 3 } \right)$

${d_2}$ có một vectơ chỉ phương là $\overrightarrow {{u_2}} = \left( {1;0} \right)$ nên ${d_2}$ có một vectơ pháp tuyến là $\overrightarrow {{n_2}} = \left( {0;1} \right)$

Góc giữa hai đường thẳng ${d_1}$ và ${d_2}$ được tính theo công thức:

$cos\left( {{d_1},{d_2}} \right) = \frac{{\left| {{{\vec n}_1} \cdot {{\vec n}_2}} \right|}}{{\left| {{{\vec n}_1}} \right| \cdot \left| {{{\vec n}_2}} \right|}} = \frac{{\left| {1 \cdot 0 – \sqrt 3 \cdot 1} \right|}}{{\sqrt {{1^2} + {{( – \sqrt 3 )}^2}} \cdot \sqrt {{0^2} + {1^2}} }} = \frac{{\sqrt 3 }}{2}$.

Vậy $\left( {{d_1},{d_2}} \right) = {30^ \circ }$.

Câu 11: Trong mặt phẳng toạ độ $Oxy$, phương trình nào dưới đây là phương trình đường tròn?

A. ${x^2} + 2{y^2} – 2x + 4y – 1 = 0$.

B. ${x^2} – {y^2} + 4x – 6y – 2 = 0$.

C. ${x^2} + {y^2} + x + y + 4 = 0$.

D. ${x^2} + {y^2} – 4x – 1 = 0$.

Lời giải

Phương trình ở hai phương án $A$ và $B$ không đúng dạng phương trình đường tròn.

Xét phương án $C$ ta có: ${\left( { – \frac{1}{2}} \right)^2} + {\left( { – \frac{1}{2}} \right)^2} – 4 = – \frac{7}{2} < 0$ nên không phải là phương trình đường tròn.

Xét phương án $D$ ta có: ${2^2} + 1 = 5 > 0$ nên là phương trình đường tròn.

Câu 12: Trong mặt phẳng tọa độ $Oxy$, cho đường tròn $\left( C \right)$ có phương trình ${x^2} + {y^2} – 2x + 4y – 4 = 0$. Tâm $I$ và bán kính $R$ của $\left( C \right)$ lần lượt là

A. $I\left( {1; – 2} \right),R = 1$.

B. $I\left( {1; – 2} \right),R = 3$.

C. $I\left( {1; – 2} \right),R = 9$.

D. $I\left( {2; – 4} \right),R = 3$.

Lời giải

Phương trình đường tròn có dạng: ${x^2} + {y^2} – 2Ax – 2By + C = 0$.

Theo đề bài ta có: $A = 1,B = – 2,C = – 4$.

Tâm $I\left( {1; – 2} \right)$.

Bán kính $R = \sqrt {{A^2} + {B^2} – C} = \sqrt {{1^2} + {{( – 2)}^2} + 4} = 3$.

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4 . Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho bảng biến thiên của hàm số bậc hai $y = a{x^2} + bx + c$. Xét tính đúng sai của các mẹnh đề sau:

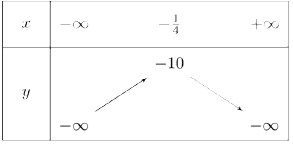
a) Hàm số đã cho nghịch biến trên khoảng $\left( {2; + \infty } \right)$.

b) Hệ số $a$ của hàm số bậc hai đã cho là một số dương

c) Hàm số đã cho đồng biến trên khoảng $\left( { – \frac{1}{4};2} \right)$.

d) Giá trị lớn nhất của hàm số bằng -10

Lời giải

a) Đúng: Hàm số đã cho nghịch biến trên khoảng $\left( {2; + \infty } \right)$.

b) Sai: Hệ số $a$ của hàm số bậc hai đã cho là một số âm

c) Sai: Hàm số đã cho đồng biến trên khoảng $\left( { – \frac{1}{4};2} \right)$.

d) Đúng: Giá trị lớn nhất của hàm số bằng -10

Câu 2: Trong mặt phẳng với hệ tọa độ $Oxy$, cho tam giác $ABC$ có phương trình cạnh $AB$ là $x – y – 2 = 0$, phương trình cạnh $AC$ là $x + 2y – 5 = 0$. Biết trọng tâm của tam giác là điểm $G\left( {3;2} \right)$.

a) Phương trình cạnh $AB$ và phương trình cạnh $AC$ có cùng một vectơ pháp tuyến.

b) Tọa độ của điểm $A$ là $A\left( {3;1} \right)$

c) Hoành độ của điểm $C$ là một số nguyên âm

d) Phương trình đường thẳng cạnh $BC$ là $x – 4y + 7 = 0$

Lời giải

Tọa độ điểm $A$ là nghiệm của hệ $\left\{ {\begin{array}{*{20}{l}}
{x – y – 2 = 0} \\
{x + 2y – 5 = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 3} \\
{y = 1}
\end{array}} \right.} \right.$ nên $A\left( {3;1} \right)$

Gọi $B\left( {b;b – 2} \right)$ và $C\left( {5 – 2c;c} \right),G$ là trọng tâm tam giác $ABC$ nên $b,c$ là nghiệm của hệ

$\left\{ {\begin{array}{*{20}{c}}
{5 – 2c + b + 3 = 9} \\
{c + b – 2 + 1 = 6}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{b = 5} \\
{c = 2}
\end{array}} \right.} \right.$.

Vậy $B\left( {5;3} \right);C\left( {1;2} \right) \Rightarrow \overrightarrow {BC} = \left( { – 4; – 1} \right)$

Một véctơ pháp tuyến của đường thẳng $BC$ là $\overrightarrow {{n_{BC}}} = \left( {1; – 4} \right)$

Suy ra phương trình đường thẳng $BC:1\left( {x – 1} \right) – 4\left( {y – 2} \right) = 0 \Leftrightarrow BC:x – 4y + 7 = 0$

$ \Rightarrow m – n = – 4 – 7 = – 11$.

a) Sai: Phương trình cạnh $AB$ và phương trình cạnh $AC$ có cùng một vectơ pháp tuyến.

b) Đúng: Tọa độ của điểm $A$ là $A\left( {3;1} \right)$

c) Sai: Hoành độ của điểm $C$ là một số nguyên âm

d) Đúng: Phương trình đường thẳng cạnh $BC$ là $x – 4y + 7 = 0$

Câu 3: Công ty $A$ có 100 cán bộ công nhân viên và muốn tổ chức cho toàn công ty đi Year End Party tại khu du lịch Tam Đảo, Vĩnh Phúc. Một công ty du lịch chào giá vé với công ty A như sau:

Với 40 khách hàng đầu tiên có giá vé là 3 triệu đồng/người.

Nếu có nhiều hơn 40 người đăng kí thì cứ thêm 1 người giá vé sẽ giảm 15000 đồng/người cho toàn bộ hành khách.

Gọi $x$ là số lượng cán bộ công nhân viên của công ty $A$ đăng kí thứ 41 trở lên. Biết chi phí thực tế công ty dành cho mỗi khách hàng là 1,95 triệu đồng.

a) Giá vé còn lại sau khi thêm $x$ người là: 3000 -15x (nghìn đồng/ người)

b) Chi phí thực tế cho chuyến đi này là: 1950(40-x) (nghìn đồng)

c) Lợi nhuận của công ty du lịch đạt được biểu thị bằng công thức $T = 15{x^2} – 450x + 42000$ (nghìn đồng)

d) Số cán bộ công nhân viên công ty $A$ đăng ký tối thiểu là 50 người thì công ty du lịch đạt lợi nhuận tối thiểu 45 triệu đồng.

Lời giải

Điều kiện: $x \in \mathbb{N}$

Vì cứ nhiều hơn 40 người đăng kí thì cứ thêm 1 người giá vé sẽ giảm 15000 đồng/người cho toàn bộ hành khách nên thêm $x$ người giá vé còn: $3000 – 15x$ (nghìn đồng/người)

Doanh thu của công ty du lịch là: $\left( {3000 – 15x} \right)\left( {40 + x} \right)$ (nghìn đồng)

Chi phí thực tế cho chuyến đi là: 1950 $\left( {40 + x} \right)$ (nghìn đồng)

Lợi nhuận của công ty du lịch đạt được là:

$T = \left( {3000 – 15x} \right)\left( {40 + x} \right) – 1950\left( {40 + x} \right)$

$T = – 15{x^2} – 600x + 3000x + 120000 – 1950x – 78000$

$T = – 15{x^2} + 450x + 42000$ (nghìn đồng)

Để lợi nhuận công ty tối thiểu là 45 triệu đồng thì

$T \geqslant 45000 \Leftrightarrow – 15{x^2} + 450x + 42000 \geqslant 45000 \Leftrightarrow – 15{x^2} + 450x – 3000 \geqslant 0 \Leftrightarrow 10 \leqslant x \leqslant 20$

Vậy số cán bộ công nhân viên công ty $A$ đăng ký tối thiểu là 50 người thì công ty du lịch đạt lợi nhuận tối thiểu 45 triệu đồng.

a) Đúng: Giá vé còn lại sau khi thêm $x$ người là: 3000 -15x (nghìn đồng/ người)

b) Sai: Chi phí thực tế cho chuyến đi này là: 1950(40+x) (nghìn đồng)

c) Sai: Lợi nhuận của công ty du lịch đạt được biểu thị bằng công thức $T = – 15{x^2} + 450x + 42000$ (nghìn đồng)

d) Đúng: Số cán bộ công nhân viên công ty $A$ đăng ký tối thiểu là 50 người thì công ty du lịch đạt lợi nhuận tối thiểu 45 triệu đồng.

Câu 4: Trong mặt phẳng $Oxy$, cho điểm $A\left( {1; – 3} \right)$ và đường thẳng $d:2x – 3y + 5 = 0$. Gọi $\Delta $ là đường thẳng đi qua điểm $A$ và tạo với đường thẳng $d$ một góc ${45^ \circ }$.

a) Một vectơ pháp tuyến của đường thẳng $d$ là $\overrightarrow {{n_d}} = \left( {2;3} \right)$

b) Khoảng cách từ điểm $A$ đến đường thẳng $d$ bằng $\frac{{\sqrt {13} }}{{13}}$

c) Đường thẳng $\Delta $ có một vectơ pháp tuyến là $\overrightarrow {{n_\Delta }} = \left( {1;5} \right)$

d) Có hai đường thẳng $\Delta $ thỏa mãn yêu cầu bài toán đặt ra.

Lời giải

Khoảng cách từ điểm $A$ đến đường thẳng $d$ là: $d\left( {A;d} \right) = \frac{{\left| {2 \cdot 1 – 3 \cdot \left( { – 3} \right) + 5} \right|}}{{\sqrt {{2^2} + {{( – 3)}^2}} }} = \frac{{16\sqrt {13} }}{{13}}$

Đường thẳng $d$ có vectơ pháp tuyến $\overrightarrow {{n_d}} = \left( {2; – 3} \right)$.

Đường thẳng $\Delta $ có vectơ pháp tuyến $\overrightarrow {{n_\Delta }} = \left( {a;b} \right),{a^2} + {b^2} > 0$.

Do $\Delta $ tạo với đường thẳng $d$ một góc ${45^ \circ }$ nên $\frac{1}{{\sqrt 2 }} = cos{45^ \circ } = \left| {cos\left( {\overrightarrow {{n_d}} ,\overrightarrow {{n_\Delta }} } \right)} \right|$

Hay $\frac{1}{{\sqrt 2 }} = \frac{{\left| {\overrightarrow {{n_d}} \cdot \overrightarrow {{n_\Delta }} } \right|}}{{\left| {\overrightarrow {{n_d}} } \right| \cdot \left| {\overrightarrow {{n_\Delta }} } \right|}} \Leftrightarrow \frac{1}{{\sqrt 2 }} = \frac{{\left| {2a – 3b} \right|}}{{\sqrt {4 + 9} \cdot \sqrt {{a^2} + {b^2}} }}$

$ \Leftrightarrow 13{a^2} + 13{b^2} = 8{a^2} – 24ab + 18{b^2}$

$ \Leftrightarrow 5{a^2} + 24ab – 5{b^2} = 0 \Leftrightarrow \left( {5a – b} \right)\left( {a + 5b} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{b = 5a} \\
{a = – 5b}
\end{array}} \right.$.

Với $b = 5a$, chọn $a = 1 \Rightarrow b = 5 \Rightarrow \overrightarrow {{n_\Delta }} = \left( {1;5} \right)$

$ \Rightarrow \Delta :1\left( {x – 1} \right) + 5\left( {y + 3} \right) = 0 \Leftrightarrow x + 5y + 14 = 0$.

Với $a = – 5b$, chọn $a = 5 \Rightarrow b = – 1 \Rightarrow \overrightarrow {{n_\Delta }} = \left( {5; – 1} \right)$

$ \Rightarrow \Delta :5\left( {x – 1} \right) – 1\left( {y + 3} \right) = 0 \Leftrightarrow 5x – y – 8 = 0$

Vậy có hai đường thẳng thỏa mãn bài toán có phương trình là: $x + 5y + 14 = 0;5x – y – 8 = 0$.

a) Sai: Một vectơ pháp tuyến của đường thẳng $d$ là $\overrightarrow {{n_d}} = \left( {2; – 3} \right)$

b) Sai: Khoảng cách từ điểm $A$ đến đường thẳng $d$ bằng $\frac{{16\sqrt {13} }}{{13}}$

c) Đúng: Đường thẳng $\Delta $ có một vectơ pháp tuyến là $\overrightarrow {{n_\Delta }} = \left( {1;5} \right)$

d) Đúng: Có hai đường thẳng $\Delta $ thỏa mãn yêu cầu bài toán đặt ra.

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1: Tìm số giao điểm giữa đồ thị hàm số $y = \sqrt {2x – 3} $ và đường thẳng $y = 3 – x$

Lời giải

Số giao điểm giữa đồ thị hàm số $y = \sqrt {2x – 3} $ và đường thẳng $y = 3 – x$ là số nghiệm của phương trình hoành độ giao điểm: $\sqrt {2x – 3} = 3 – x$

$ \Leftrightarrow {(\sqrt {2x – 3} )^2} = {(3 – x)^2} \Leftrightarrow 2x – 3 = {x^2} – 6x + 9 \Leftrightarrow {x^2} – 8x + 12 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2} \\
{x = 6}
\end{array}} \right.$.

Thay lần lượt $x = 2;x = 6$ vào phương trình $\left(*\right)$ ta thấy $x = 2$ thoả mãn.

Vậy đồ thị hàm số $y = \sqrt {2x – 3} $ và đường thẳng $y = 3 – x$ có 1 giao điểm chung.

Câu 2: Cho tam thức bậc hai $f\left( x \right) = {x^2} – \left( {2m + 3} \right)x + {m^2} + 3m$, $m$ là tham số. Có bao nhiêu giá trị nguyên của tham số $m$ để $f\left( x \right) < 0,\forall x \in \left( { – 1;0} \right)$.

Lời giải

Ta có: $f\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = m} \\
{x = m + 3}
\end{array}} \right.$.

$f\left( x \right) < 0 \Leftrightarrow x \in \left( {m;m + 3} \right)$

Do đó: $f\left( x \right) < 0,\forall x \in \left( { – 1;0} \right) \Leftrightarrow \left( { – 1;0} \right) \subset \left( {m;m + 3} \right)$

$ \Leftrightarrow m \leqslant – 1 < 0 \leqslant m + 3 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m \leqslant – 1} \\
{0 \leqslant m + 3}
\end{array}} \right.$.

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m \leqslant – 1} \\
{ – 3 \leqslant m}
\end{array} \Leftrightarrow – 3 \leqslant m \leqslant – 1} \right.$

Vậy $ – 3 \leqslant m \leqslant – 1 \Rightarrow m \in \left\{ { – 3; – 2; – 1} \right\}$ nên có 3 giá trị nguyên thỏa mãn.

Câu 3: Độ giảm huyết áp của một bệnh nhân được cho bởi công thức $G\left( x \right) = 0,3x\left( {12 – x} \right)$, trong đó $x$ là liều lượng thuốc được tiêm cho bệnh nhân ( $x$ được tính bằng miligam). Tính liều lượng thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.

Lời giải

Điều kiện: $x \in \left[ {0;12} \right]$ (vì độ giảm huyết áp không thể là số âm).

Độ giảm huyết áp của một bệnh nhân được cho bởi công thức $G\left( x \right) = 0,3x\left( {12 – x} \right)$

$ \Leftrightarrow G\left( x \right) = 3,6x – 0,3{x^2}$ đây là một hàm số bậc hai.

Do $a = – 0,3 < 0$ nên hàm số đồng biến trên khoảng $\left( { – \infty ;6} \right)$ và nghịch biến trên khoảng $\left( {6; + \infty } \right)$ và có bảng biến thiên như sau:

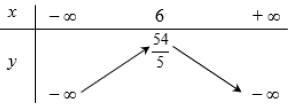
Vậy huyết áp bệnh nhân giảm nhiều nhất khi tiêm cho bệnh nhân liều $x = 6$ miligam.

Câu 4: Cho tam giác $ABC$ với $A\left( { – 1; – 2} \right)$ và phương trình đường thẳng chứa cạnh $BC$ là $x – y + 4 = 0$ Phương trình đường trung bình ứng với cạnh đáy $BC$ của tam giác có dạng $ax + by + c = 0$. Hãy tính giá trị của biểu thức $T = a + b + c$.

Lời giải

Chọn điểm $K\left( {0;4} \right)$ thuộc $BC$ và gọi $E$ là trung điểm đoạn $AK$ nên $E\left( { – \frac{1}{2};1} \right)$.

Gọi $d$ là đường trung bình ứng với cạnh đáy $BC$ của tam giác $ABC$, suy ra $d$ qua $E$ và có một vectơ pháp tuyến $\overrightarrow {n’} = \left( {1; – 1} \right)$.

Phương trình tổng quát $d:1\left( {x + \frac{1}{2}} \right) – 1\left( {y – 1} \right) = 0$ hay $2x – 2y + 3 = 0$.

Vậy $\left\{ {\begin{array}{*{20}{l}}
{a = 2} \\
{b = – 2} \\
{c = 3}
\end{array} \Rightarrow T = a + b + c = 2 – 2 + 3 = 3} \right.$.

Câu 5: Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng $\Delta :ax + by + 4 = 0\left( {a,b \in \mathbb{N}} \right)$ đi qua điểm $M\left( { – 1; – 2} \right)$ và tạo với đường thẳng $d:x + 3y – 3 = 0$ một góc $\frac{\pi }{4}$. Giá trị biểu thức $P = a + b$ bằng

Lời giải

Đường thẳng $\Delta :ax + by + 4 = 0\left( {a,b \in \mathbb{N}} \right)$ đi qua điểm $M\left( { – 1; – 2} \right)$

Ta có: $ – a – 2b + 4 = 0 \Rightarrow a = 4 – 2b$.

Suy ra $\Delta :\left( {4 – 2b} \right)x + by + 4 = 0$

Khi đó: $cos\frac{\pi }{4} = \frac{{\left| {4 – 2b + 3b} \right|}}{{\sqrt {{{(4 – 2b)}^2} + {b^2}} \cdot \sqrt {{1^2} + {3^2}} }}$

$ \Leftrightarrow \frac{1}{{\sqrt 2 }} = \frac{{\left| {4 + b} \right|}}{{\sqrt {5{b^2} – 16b + 16} \cdot \sqrt {10} }}$

$ \Leftrightarrow 5\left( {5{b^2} – 16b + 16} \right) = {(4 + b)^2}$

$ \Leftrightarrow 24{b^2} – 88b + 64 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{b = 1} \\
{b = \frac{8}{3}\left( L \right) do\,b \in \mathbb{N}}
\end{array}} \right.$

Với $b = 1 \Rightarrow a = 2$. Vậy $P = a + b = 3$.

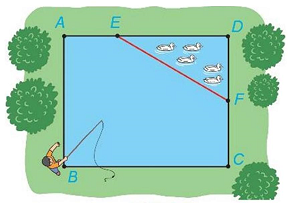
Câu 6: Một ao cá có dạng hình chữ nhật $ABCD$ với chiều dài $AD = 17\;m$, chiều rộng $AB = 13\;m$.

Phần tam giác $DEF$ người ta để nuôi vịt, biết $AE = 6\;m,CF = 6,5\;m$ (minh họa như hình vẽ).

Tính khoảng cách từ vị trí người đứng ở vị trí $B$ câu cá đến vách ngăn nuôi vịt là đường thẳng $EF$ (Kết quả làm tròn đến hàng phần trăm).

Lời giải

Chọn hệ trục toạ độ $Oxy$, có điểm $O$ trùng với điểm $B$, các tia $Ox,Oy$ tương ứng trùng với các tia $BC,BA$. Chọn 1 đơn vị độ dài trên mặt phẳng toạ độ tương ứng với $1\;m$ trong thực tế.

Khi đó $A\left( {0;13} \right),B\left( {0;0} \right),C\left( {17;0} \right),D\left( {17;13} \right),E\left( {6;13} \right),F\left( {17;6,5} \right)$.

$\overrightarrow {EF} \left( {11; – 6,5} \right)$.

Đường thẳng $EF$ có vectơ chỉ phương là $\overrightarrow {EF} \left( {11; – 6,5} \right)$ nên có vectơ pháp tuyến $\vec n = \left( {6,5;11} \right)$ và đi qua điểm $E\left( {6;13} \right)$.

Suy ra phương trình tổng quát của đường thẳng $EF$ là: $6,5\left( {x – 6} \right) + 11\left( {y – 13} \right) = 0$

$ \Leftrightarrow 6,5x + 11y – 182 = 0$.

Khoảng cách từ $B$ đến đường thẳng $EF$ là $d\left( {B,EF} \right) = \frac{{\left| { – 182} \right|}}{{\sqrt {6,{5^2} + {{11}^2}} }} \approx 14,24$.

Vậy khoảng cách từ vị trí người đứng ở vị trí $B$ câu cá đến vách ngăn nuôi vịt là đường thẳng $EF$ bằng 14,24 mét.